Wiskunde rond de wereld

We zijn net terug van onze huwelijksreis: een trip langs de zeven culturele wereldwonderen.
Het was een fantastische reis waarvan we voor vrienden en kennissen een verslag hebben gemaakt op polarsteps. Tijdens deze reis heb ik presentaties gegeven aan onze groep over wiskunde, gelinkt aan de zeven wereldwonderen die we hebben bezocht. Tot mijn verbazing bleef de hele groep geïnteresseerd in mijn verhaaltjes en dat is mede de reden dat ik heb besloten ze uit te schrijven en ze hier op mijn website te zetten. Blijkbaar is het me gelukt om over te brengen dat wiskunde meer is – of eigenlijk in mijn optiek iets anders is – dan sinussen en cosinussen, integralen en afgeleiden. Wiskunde is een manier van denken, van problemen oplossen, van tegen de wereld aan kijken, die verschillende culturen hebben gebruikt om grip te krijgen op hun omgeving, de toekomst te kunnen voorspellen en/of hun samenleving te organiseren. En misschien is wiskunde nog wel veel meer dan dat, maar nu loop ik op de zaken vooruit. Laten we beginnen bij onze eerste stop…
Rio de Janeiro / Brazilië / Artur Avila
Het eerste wereldwonder dat we bezochten was het Christo Redentor beeld in Rio de Janeiro. Maar Rio is ook de woonplaats van één van de meest veelbelovende jonge wiskundigen van vandaag: Artur Avila.

Artur is zeker niet onaardig om te zien, wat je niet van alle wiskundigen kunt zeggen, maar hij is wel een beetje vreemd, wat je van heel veel wiskundigen kunt zeggen. Zo heeft hij heel lang geweigerd om een auto of fiets aan te schaffen. Hij weet namelijk van zichzelf dat hij op onverwachte momenten een ingeving kan krijgen over een wiskundig probleem waaraan hij werkt, en dan zo op kan gaan in zijn gedachten daarover dat hij totaal niet meer oplet wat er om hem heen gebeurt. In zo’n situatie een ongeval veroorzaken zou hij zichzelf nooit vergeven. Zijn beste ideeën krijgt hij aan het strand en dus selecteerde hij een tijd lang wiskundige conferenties die gehouden werden in een hotel dat aan het strand lag. Nu is de situatie omgekeerd: als de organisatie van een conferentie wil dat Avila komt, zoeken ze een hotel uit dat aan het strand ligt. Een vrouwelijke collega wiskundige heeft ooit gezegd dat als je met Artur wilt samenwerken je in ieder geval moet zorgen voor een goed badpak. Hij zegt van zichzelf dat geen enkele baas hem in dienst zou willen, maar in de wiskunde is hij inmiddels een grote ster. Hij is de eerste Zuid-Amerikaan die ooit de prestigieuze Fields Medaille heeft gewonnen.
De Fields Medaille is een soort Nobelprijs voor de wiskunde. (Het is eigenlijk vreemd dat er geen Nobelprijs voor de wiskunde bestaat, wel voor natuurkunde, scheikunde, geneeskunde, literatuur en de vrede.) De prijs is genoemd naar de Canadese wiskundige John Charles Fields, die zijn leven lang (van 1863 tot 1932) zijn best deed om de aandacht voor wiskunde en wiskundeonderwijs in de wereld te vergroten. Bij zijn dood liet hij 47.000 dollar na voor een fonds waaruit elke 4 jaar een prijs voor de meest veelbelovende jonge wiskundigen moest worden gefinancierd. Er zijn wel wat verschillen met de Nobelprijzen. Zo mag een Fields Medalist niet ouder zijn dan 40. Op die regel is slechts één keer een uitzondering gemaakt. In 1998 kreeg Andrew Wiles een bijzondere Fields Medaille voor zijn bewijs van de laatste stelling van Fermat. Wiles was toen 44, en we zullen zijn naam nog tegenkomen in het verhaal over India.
Het werk van Artur Avila is lastig te omschrijven, je kunt het met recht hogere wiskunde noemen. En ik moet eerlijk toegeven dat een titel als “Absolute continuity of the integrated density of states for the almost Mathieu operator with non-critical coupling” voor mij ook abacadabra is. Maar ik kan wel proberen iets uit te leggen over één van zijn grote successen (waarnaar de titel die ik net gaf verwijst). Het heeft allemaal te maken met zogenaamde dynamische systemen.
Dynamische systemen zijn systemen die veranderen of zich ontwikkelen in de tijd. Een simpel voorbeeld van een dynamisch systeem is een slinger; een balletje aan een stokje. Als je het balletje een zetje geeft gaat het heen en weer slingeren. Die beweging is een verandering van de plaats van het balletje in de tijd en dus is dit een dynamisch systeem. Maar ook het weer, met luchtdruk, temperatuur, luchtvochtigheid en nog een reeks grootheden, die veranderen in de tijd, of de effectenbeurs met aandelenkoersen die veranderen in de tijd, zijn voorbeelden van dynamische systemen. Om heel precies te zijn, zijn voor wiskundigen niet de slinger, het weer en de beurs de dynamische systemen, maar de formules en vergelijkingen die de bewegingen en veranderingen beschrijven.
Één van de meest bestudeerde onderwerpen in het vakgebied van de dynamische systemen is chaos. Nu is het zo dat de betekenis van begrippen in de wiskunde niet altijd helemaal overeen komt met de betekenis die die begrippen in het dagelijks leven hebben. Beter gezegd: begrippen in de wiskunde moeten heel exact gedefinieerd zijn (en dat moet ook in alle andere wetenschappen), terwijl in het dagelijks leven de betekenis nog wel eens wil variëren. Zo kan mijn moeder vinden dat mijn slaapkamer vroeger regelmatig een chaos was, terwijl ik dat zelf heel erg mee vind vallen. In de wiskunde is chaos gedefinieerd als ‘een extreme afhankelijkheid van begincondities’[1]. Wat dat inhoudt kan ik laten zien aan de hand van het simpele voorbeeld van de slinger. De beweging van de slinger is heel regelmatig en voorspelbaar, een zich steeds herhalende heen-en-weer beweging. Vanwege die herhaling noemen we de beweging periodiek, na een vaste periode herhaalt zich hetzelfde patroon. Maar als we die simpele slinger een klein beetje ingewikkelder maken door er een tweede slinger onderaan te hangen krijgen we ineens een heel ander beeld.
[1] Dit is eigenlijk maar één van de definities. Er zijn ook andere, maar dit is de meest gebruikte.
De beweging wordt nu onregelmatig en is niet meer periodiek. Het is goed om hier op te merken dat de beweging niet onvoorspelbaar is. We kunnen de vergelijkingen waaraan het dubbele slingersysteem zich moet houden makkelijk opschrijven en het filmpje is eigenlijk het resultaat van een simulatie, een berekening gebaseerd op die vergelijkingen. Voor iedere beginpositie kunnen we uitrekenen hoe de beweging er uit komt te zien. Maar dat berekenen moet wel heel erg precies gebeuren en het bepalen van de beginpositie ook.
Het filmpje hierboven laat drie keer (in groen, rood en blauw) de beweging van dezelfde dubbele slinger zien maar met net heel iets andere beginposities. Aanvankelijk lijken de bewegingen erg op elkaar, maar na verloop van tijd gaan de drie slingers heel verschillende dingen doen. Een heel klein verschil in het begin leidt na verloop van tijd tot grote verschillen, een ‘extreme afhankelijkheid van de begincondities’.
Dit chaotische gedrag werd al in de 19e eeuw opgemerkt door o.a. Henri Poincaré en Jacques Hadamard, maar het was de Amerikaanse wiskundige Lorenz die het in 1961 pas officieel beschreef als ‘extreme afhankelijkheid van de begincondities’. Lorenz werkte aan weersvoorspellingen, die tot dan toe vooral beperkt werden door de enorme hoeveelheid berekeningen die nodig waren om de vergelijkingen in voldoende detail door te rekenen. Met de introductie van de computer was de verwachting dat de weersvoorspellingen snel beter zouden worden. Maar tot de grote frustratie van met name de wiskundigen die aan de weersmodellen werkten, lukte dat niet. Hoewel de voorspellingen voor een dag of drie vooruit wel verbeterden, ging het bij een dag of 5 à 6 nog altijd hopeloos mis. En hoe preciezer de metingen die ingevoerd werden en hoe nauwkeuriger de modellen, het maakte niets uit voor die langere-termijn-voorspellingen. Tot Lorenz op een dag besloot een deel van zijn berekeningen opnieuw te draaien op zijn Royal McBee LGP-30 computer. Lorenz printte de uitkomst na een aantal dagen uit op papier en voerde de waarden als beginwaarden in voor een nieuwe berekening. De nieuwe berekening leek aanvankelijk precies op de complete simulatie die hij daarvoor had gedraaid, maar na een dag begonnen er kleine verschillen zichtbaar te worden, en na nog een dag leken de twee oplossingen die hetzelfde hadden moeten zijn helemaal niet meer op elkaar (net als bij de dubbele slingers met iets verschillende beginposities). Zoals een echte wiskundige betaamt ging Lorenz op zoek naar de oorzaak, en ontdekte dat de cijfers die hij had uitgeprint en ingevoerd afgerond waren. De computer rekende met getallen met 6 cijfers achter de komma, maar de standaard printout gaf maar 3 cijfers achter de komma. Deze kleine afrondingen kun je zien als kleine verstoringen op de ‘echte’ waarden, en die bleken in het weermodel alsmaar te groeien totdat ze de oplossing totaal domineerden. Lorenz zelf heeft het op een conferentie als volgt beschreven: “de vleugelslag van een vlinder in Brazilië kan een wervelstorm in Texas veroorzaken”.
Nu is de beweging van een dubbele slinger niet altijd chaotisch. Als we bijvoorbeeld de onderste bal heel zwaar maken en de bovenste heel licht, dan ontstaat in feite één lange slinger met een klein balletje halverwege het stokje. De beweging is dan een periodieke, zoals van een enkele slinger, met een kleine verstoring die niet groter wordt. Als we de verhouding tussen de massa van de bovenste bal en de onderste bal langzaam laten veranderen van een heel klein getal (grote onderste massa en kleine bovenste) naar 1 (gelijke massa’s), dan gaat het gedrag ergens over van periodiek naar chaotisch. De vraag die wiskundige al lange tijd bezig houdt is: is er sprake van één enkele overgang, of is er een soort van tussengebied waarin periodiek en chaotisch gedrag elkaar afwisselen? In het filmpje hieronder is een voorbeeld te zien van een systeem dat van periodiek overgaat in chaotisch, en duidelijk is te zien dat er een overgangsgebied is waarin chaotisch en periodiek gedrag elkaar afwisselen. Maar geldt dat voor alle dynamische systemen die ergens periodiek en ergens chaotisch gedrag vertonen?
Artur Avila heeft aangetoond dat dit inderdaad geldt voor een hele grote klasse dynamische systemen, waarvan bekend was dat ze een gebied met chaotisch en een gebied met periodiek gedrag hebben. Al deze systemen hebben dus een overgangsgebied waarin chaotisch gedrag en periodiek gedrag elkaar afwisselen. (Een wiskundige heeft dit eens beschreven als ‘een zee van chaos met eilandjes van periodiciteit’.) Het bewijzen hiervan is een grote wiskundige prestatie en Artur heeft er zo nog een paar op zijn naam. Maar de vraag rijst misschien “wat hebben we hier nu aan?”. In de wiskunde is dat niet altijd gemakkelijk te zeggen. In een later verhaal zal ik aangeven dat een stelling waarvan de geschiedenis terug gaat tot de 6e eeuw, pas in de 21e eeuw een toepassing heeft gevonden en nu door bijna iedereen wordt gebruikt. Maar in het geval van het werk van Artur Avila aan het overgangsgebied tussen periodiek en chaotisch gedrag is er wel een direct nut. In de financiële wereld wordt ontzettend veel gebruik gemaakt van wiskundige modellen. Die modellen behoren vaak tot de klasse waarover Artur’s bewijs gaat, ze hebben een gebied waarin ze periodiek gedrag vertonen (koersen gaan vaak op en neer met een zekere regelmaat) en een gebied waarin het gedrag chaotisch is. Dat chaotische gedrag kan tot grote problemen leiden omdat koersen dan erg onvoorspelbaar gaan lijken en kleine veranderingen in bijvoorbeeld het koopgedrag enorme gevolgen kunnen hebben. De financiële instellingen willen dus graag in het periodieke gebied blijven. Maar de ‘snelle financiële jongens’ die bij die instellingen werken weten dat hoe dichter je bij het chaotische gebied komt, hoe interessanter het wordt (lees: hoe meer er voor hen valt te verdienen). Omdat de modellen erg complex zijn is het niet mogelijk om af te leiden waar de grens van het periodieke gebied ligt. Daarom worden simulaties gedraaid met de modellen met als simpele regel: ‘als de uitkomst periodiek is zitten we in het periodieke gebied, en als de uitkomst chaotisch is zitten we in het chaotische gebied’.

Artur Avila’s werk laat zien dat deze regel te simpel is en dat beide uitkomsten ook kunnen betekenen dat we in het overgangsgebied zitten. En als dat zo is kan een kleine wijziging van het systeem, bijvoorbeeld door veranderingen in de financiële regelgeving of door de uitvinding van een nieuw beleggingsproduct, ineens tot chaos leiden. Er wordt wel beweerd dat de financiële crisis van een paar jaar geleden voor een deel te wijten is aan een te groot vertrouwen in het ‘nette gedrag’ van financiële modellen. Daarmee wordt het werk van wiskundigen als Artur Avila voor ons allemaal van groot belang.
Machu Picchu / de Inca’s / de Yupana

Ons tweede wereldwonder was Machu Picchu, de wonderlijke Inca-stad die in 1911 ontdekt werd door Hiram Bingham (die eigenlijke op zoek was naar het legendarische Vilcabamba, de stad waar de laatste Inca’s hun toevlucht zouden hebben gezocht voor de Spaanse conquistadors). Voor veel onderzoekers is het nog steeds een raadsel hoe het de Inca’s[1] is gelukt om in een hele korte periode van minder dan 100 jaar een gigantisch rijk op te bouwen dat zo’n 2 miljoen vierkante kilometer omvatte en waar ongeveer 10 miljoen mensen woonden. En dat alles zonder het gebruik van rijdieren, het wiel of het schrift. Elders beschrijf ik dat daar tegenwoordig wel aardige ideeën over zijn, maar de vraag blijft hoe de Inca hun rijk bestuurden, hoe ze de mankracht organiseerden voor de gigantische bouwprojecten en hoe ze die gebouwen konden uitlijnen. Daarvoor is wiskunde nodig, je moet in staat zijn complexe berekeningen te maken. Optellen en aftrekken is niet genoeg, je moet minstens ook kunnen vermenigvuldigen en delen. Hoe de Inca’s dat deden is heel lang een raadsel geweest. Eigenlijk wisten we niet erg veel meer dan dat de Inca’s rekenmeesters hadden en dat die een zogenaamde yupana gebruikten. Gelukkig hebben we een afbeelding van zo’n yupana, gemaakt door een Quecha adellijke meneer Guaman Poma de Ayala, maar hij beschrijft niet in genoeg detail hoe deze wordt gebruikt[2].
[1] Eigenlijk is de term Inca’s verkeerd. De mensen die wij aanduiden als Inca’s noemden zichzelf Quecha, en alleen hun koning noemden ze Inca. Ik zal me hier niet strikt aan houden en de namen door elkaar gebruiken.
[2] De tekening staat in een geschrift getiteld El primer nueva corónica y buen gobierno oftewel de eerste nieuwe kroniek en goede regering. Het is een lange aanklacht gericht aan koning Filips III van Spanje over de wijze waarop de Quecha werden behandeld door de Spaanse veroveraars. Gelukkig beschrijft Huaman Poma in detail allerlei aspecten van het leven van de Quecha, en het boek bevat maar liefst 398 prachtige pentekeningen.

Tot mijn verbazing zag ik in een winkel in Aquas Calientes een spel genaamd Yupana Inka, met op de achterkant ‘ontdek de mysterieuze en geheime wiskunde van de Inca’s’. Ik heb het spel niet gekocht, mede omdat uit de omschrijving op de achterkant al blijkt dat ik er waarschijnlijk niet veel wijzer van zou zijn geworden over hoe de Inca’s de yupana gebruikten. Dat heeft er niets mee te maken dat de Inca’s hun wiskunde geheim zouden hebben gehouden. Naast Poma de Ayala heeft ook de Spaanse missionaris Jose de Acosta in zijn “La Historia Natural y Moral de Las Indias” het gebruik van de yupana beschreven. De Inca-rekenmeesters vonden het blijkbaar geen enkel probleem om te laten zien hoe ze de yupana gebruikten aan één van hun Spaanse overheersers. De wiskunde van de Inca’s is dus niet zozeer geheim, maar wel mysterieus. En dat komt omdat geen van de beschrijvingen inzicht geeft in de manier waarop de yupana werd gebruikt. Acosta is duidelijk totaal niet wiskundig onderlegd. Hij is onder de indruk van de snelheid waarmee de Inca-rekenmeesters complexe berekeningen uitvoeren en geeft aan dat ze dat doen zonder fouten (en beter dan de Spaanse rekenmeesters), en dat ze maiskorrels gebruiken die ze op de yupana verplaatsen, maar het is duidelijk dat Acosta geen flauw idee heeft waarom “ze er één hier plaatsen en drie ergens anders en acht ik weet niet waar”.
Je zou zeggen dat het verhaal daarmee afgelopen is. Zonder beschrijving van het gebruik van de yupana en met alleen maar een tekening is het onmogelijk om er achter te komen hoe de Inca’s hun berekeningen uitvoerden? Toch? Nee dus. Als er iets is waar wiskundigen van houden en waar ze goed in zijn dan is het het oplossen van puzzels, en dit is een fantastische puzzel. Veel wiskundigen – vooral uit de Inca-regio – hebben zich dan ook al bezig gehouden met het oplossen van die puzzel. En in 2010 is het een wiskunde-professor in Minnesota samen met een studente Spaans met een voorliefde voor de wiskunde van de Inca’s gelukt om de puzzel op te lossen[1]! Hoe hebben ze dat gedaan?
[1] Leonard, M., and Shakiban, C. “on The Incan Abacus: A Curious Counting Device”, Journal of Mathematics and Culture, Volume 5 Number 2, November 2010.
Het begint met een stukje logisch nadenken. Zoals ik al aangaf moeten de Inca’s hebben kunnen optellen, aftrekken, vermenigvuldigen en delen. Dat moet dus allemaal met de yupana mogelijk zijn. Het optellen (en aftrekken) is niet zo moeilijk. De Chinezen gebruiken daar een telraam voor en ook wij Europeanen hebben dat eeuwenlang gedaan. Bovendien beschrijft Huaman Poma dat de Inca’s een tientallig stelsel gebruikten. Tenslotte weten we dat de Inca’s getallen vastlegden met behulp van zogenaamde quipu (zie https://nl.wikipedia.org/wiki/Quipu voor meer informatie) met knopen die eenheden voorstelden, tientallen, honderdtallen, duizendtallen etc. Dat de yupana op een vergelijkbare manier zou zijn opgedeeld, waarbij de onderste rij voor de eenheden is, die daarboven voor de tientallen, daarboven voor de honderdtallen, etc.
Nu is alleen nog de vraag waarom elke rij elf gaatjes/vakjes heeft in plaats van tien (5+3+2+1), zoals de kralen op een telraam[1]. De functie van het extra gaatje – in de rechterkolom – is niet zo ingewikkeld om te bedenken. Bij het optellen kan het voorkomen dat in bijvoorbeeld de rij van de eenheden tien vakjes vol raken, maar dat er eigenlijk nog meer eenheden bij moeten. We kunnen dan ruimte maken door de tien eenheden te vervangen door één tiental. Op de yupana komt dat er op neer dat we één maiskorreltje in de rechterkolom plaatsen – om te onthouden dat er tien eenheden waren – en dan mogen we de rij voor de eenheden verder weer leeg maken. Als dat is gebeurd verplaatsen we het maiskorreltje uit de rechterkolom naar de rij erboven. (Voor degenen die zich het optellen van grote getallen op de lagere school nog herinneren: dit komt overeen met het één onthouden.)
[1] Strikt genomen heb je aan negen gaatjes genoeg omdat je de getallen 0 t/m 9 weer moet kunnen geven.
Het gebruik van een extra kolom rechts alleen maar om te onthouden dat we tien eenheden vervangen door één tiental, lijkt wat overdreven. Het leegmaken van de rij eenheden en het plaatsen van een maiskorreltje extra in de rij van de tientallen kan best in één keer worden gedaan, zoals op een telraam gebeurt. Maar dat is wel wat foutgevoeliger. Als de rekenaar tijdens deze bewerking gestoord wordt is er een kans dat er vergeten wordt een extra korreltje in de rij tientallen te plaatsen. Omdat bij de yupana alle informatie op het bord blijft is de kans dat er iets fout gaat kleiner. En dit zou kunnen verklaren waarom zowel Huaman Poma als de Acosta benadrukken dat de Inca rekenmeesters zo weinig fouten maken. In figuur 1 wordt een voorbeeld gegeven van optellen met de yupana.

Figuur 1: voorbeeld van optellen met de yupana. In stap C wordt een ‘volle’ rij met 10 steentjes vervangen door één steentje in de rechterkolom. In stap E wordt dit ene steentje verplaatst naar de rij erboven.
Aftrekken is omgekeerd optellen en zal ik hier niet uitvoerig uitleggen. Figuur 2 geeft een voorbeeld en ook hier zien we het gebruik van de rechterkolom voor het vervangen van één honderdtal door tien tientallen.

Figuur 2: Aftrekken met behulp van de yupana. In stap D wordt een steentje van de honderdtallen-rij naar de rechterkolom een rij lager verplaatst, omdat deze rij leeg is geraakt. In stappen E en F wordt dit steentje vervangen door een ‘volle’ rij met tien steentjes. Vervolgens kunnen er vijf steentjes naar de linkerkant van de yupana worden verplaatst om links en rechts van de yupana dezelfde aantallen te krijgen.
Maar nu wordt het ingewikkeld (en daarom interessant): hoe kun je vermenigvuldigen met de yupana? Zoals aangegeven moet dit wel met de yupana mogelijk zijn geweest, maar vermenigvuldigen met een soort telraam, hoe kan dat? Er zijn (o.a. op youtube) wel manieren te vinden om te vermenigvuldigen en daarbij een telraam te gebruiken, maar als je iets beter kijkt zie je dat hierbij de vermenigvuldiging in stukjes wordt gehakt. Elke deelvermenigvuldiging wordt ‘uit het hoofd’ gedaan, en het telraam wordt gebruikt om de deelresultaten bij elkaar op te tellen. Het kan natuurlijk zijn dat de Inca’s het ook zo hebben gedaan, maar dat lijkt niet zo logisch. Voor het ‘uit het hoofd’ doen van de deelvermenigvuldigingen is het noodzakelijk dat je de vermenigvuldigingstafels uit je hoofd kent. (Vandaar dat er in ons rekenonderwijs zo’n nadruk ligt op het uit je hoofd leren van die tafels.) Er is geen enkele aanwijzing dat de Inca’s zulke vermenigvuldigingstafels gebruikten. Maar bovendien staat het gedeeltelijk ‘uit het hoofd’ doen van een berekening nogal haaks op het gebruik van de rechterkolom bij het optellen en aftrekken. Het idee hierachter is dat alle informatie op het bord blijft en er niets ‘uit het hoofd’ gedaan hoeft te worden. Dus waarom zou dat idee bij het vermenigvuldigen – een complexere berekening – worden losgelaten? Niet logisch…
Maar we hebben nog een belangrijk gegeven van de yupana niet gebruikt. De tien gaatjes in de drie rechterkolommen zijn opgedeeld in vijf, drie en twee gaatjes. En die getallen zijn bijzonder[1]. We kunnen namelijk twee ‘maken’ door twee enen bij elkaar op te tellen, drie door twee en één bij elkaar op te tellen en vijf door drie en twee bij elkaar op te tellen. Bovendien kunnen we alle getallen tussen nul en negen schrijven als een som van de getallen vijf, drie, twee en één. Dit klinkt allemaal erg interessant, maar wat heeft het met vermenigvuldigen te maken? En hier hebben de dames Molly Leonard en Cheri Shakiban hun wiskundige inzicht gebruikt. De vraag ‘hoe gebruik je een yupana voor vermenigvuldigen?’ kun je namelijk ook stellen als ‘hoe gebruik je een instrument waarmee je kunt optellen, om mee te vermenigvuldigen?’, of ‘hoe kun je – op een handige manier – een vermenigvuldiging omzetten in een serie optellingen?’. Een vermenigvuldiging is natuurlijk eigenlijk altijd een vorm van herhaald optellen. Als ik bijvoorbeeld 153x47 wil uitrekenen, dan kan ik dat doen door 153 bij 153 op te tellen, en dan bij het resultaat weer 153 op te tellen en zo nog 44 keer te herhalen. Maar dat is niet echt een handige manier. Maar je kunt 47 ook schrijven als 40+7 of 4x10+7, en vervolgens als (3+1)x10 + (5+2), waarbij we de getallen 1, 2, 3 en 5 tevoorschijn zien komen.
[1] Ze zijn zo bijzonder dat we ze in het laatste verhaal, over de wiskunde van Italië, nog een keer zullen tegenkomen.

Figuur 3: Het getal 47 kan worden geschreven als (3+1)x10 + (5+2), door op de yupana de steentjes per rij zo te verdelen dat er alleen volle vakjes ontstaan.
Op de yupana komt dat er op neer dat we 47 neerleggen en vervolgens in elke rij zorgen dat we alleen maar geheel gevulde vakjes krijgen. Dan vinden we op de rij van de tientallen de 3 en de 1 en op de rij van de eenheden de 5 en de 2. Maar nu zijn we er nog (lang) niet. We hebben nu kolommen nodig aangeven met de cijfers 1, 2, 3 en 5. In de kolom met de 1 plaatsen we het getal 153. In de kolom met de 2 plaatsen we 2x153, wat we kunnen berekenen als 153+153=306. Het optellen kunnen we doen met een yupana zoals eerder uitgelegd. De kolom met de 3 moet 3x153 gaan bevatten en dat kunnen we uitrekenen als 306+153=459. Als laatste vullen we in de kolom met de 5 het resultaat in van 459+306=765.
Na al deze voorbereiding kunnen we – eindelijk – onze eindberekening uit gaan voeren (geillustreerd in de figuur hieronder). We beginnen op de rij van de tientallen met het getal 3. (Nog even herhalen: 47 = (3+1)x10 + (5+2), dus we hebben voor de tientallen 3+1, en voor de eenheden 5+2.) Daarvoor schuiven we de inhoud van de kolom met cijfer 3 een rij naar boven en liggen die dan in een lege yupana (stap A). Dan tellen we daar de inhoud van de kolom met cijfer 1, ook een rij naar boven verschoven, bij op (stap B). Vervolgens gaan we naar de rij met de eenheden en daar vinden we 5+2. Dus tellen we nu de inhoud van de kolom met cijfer 5 – niet verschoven – op bij de inhoud van de yupana (stap C) en tenslotte de inhoud van de kolom met cijfer 2 (stap D). De getallen die boven de kolommen staan leggen we (op de juiste rij) telkens links naast de yupana, waardoor daar het getal 47 ontstaat. En in de yupana komen we uit op 7191 = 47x153 = 4590+1530+765+306.

Figuur 4: De
vermenigvuldiging 153x47 uitgevoerd op de yupana door 4590 (10x3x153), 1530 (10x1x153), 765 (5x153) en 306 (2x153) bij elkaar op te tellen.
Op deze manier vermenigvuldigen lijkt voor ons misschien ingewikkeld en omslachtig omdat we zo gewend zijn aan onze eigen methode. Maar met wat oefenen is dit best een snelle en handige methode. Het gebruik van de getallen 1, 2, 3 en 5 blijkt erg efficiënt. Het is niet voor niets dat veel landen in hun munten en briefgeld vaak als waarden 1, 2, 5, 10, 20 en 50 of 1, 2.5, 5, 10, 25 en 50 gebruiken. Met deze getallen is efficiënt, dus met zo min mogelijk munten en briefjes, ieder bedrag samen te stellen. En bij onze westerse manier van vermenigvuldigen (zonder rekenmachine) maken we sterk gebruik van de tafels van vermenigvuldiging. Om vermenigvuldigingen met grote getallen te kunnen uitrekenen is het essentieel dat je de tafels uit je hoofd kent. Vandaar het oeverloos opdreunen van die tafels op de lagere school. Dat is bij het rekenen met de yupana niet nodig.
Uiteraard is het ook mogelijk om de yupana te gebruiken om te delen, maar dat zal ik niet helemaal uitschrijven. De laatste figuur illustreert hoe dat werkt en voor een beschrijving verwijs ik mijn geïnteresseerde lezers graag naar het werk van Molly Leonard en Cheri Shakiban: “on The Incan Abacus: A Curious Counting Device” in het Journal of Mathematics and Culture, Volume 5 Number 2, November 2010.

Figuur 5: Delen met
de yupana door gebruik te maken van de veelvouden van 153: 153 (1x153), 306 (2x153), 459 (3x153) en 765 (5x153). In stappen A-C wordt 3x10x153 van 7191 afgetrokken, als grootste factor kleiner
dan 7191. In D-F volgt 1x10x153, in G-I 5x153 en tenslotte in J en K 2x153. Aan de rechterkant ontstaat zo als resultaat 30+10+5+2=47.
Overigens stopt het verhaal van de dames Leonard en Shakiban hier nog niet. Één van beide dames - Cheri Shakiban - was studente Spaans en heeft gezocht naar verwijzingen in de dialecten van Zuid-Amerika naar de manier waarop de yupana werd gebruikt. Net zoals we in onze taal soms verwijzen naar onze manier van rekenen, bijvoorbeeld als we zeggen dat we zaken “eens goed onder elkaar moeten zetten” of dat we willen weten wat “het resultaat onder de streep” is, zo moet dat ook in de wereld van de Inca’s gebeurd zijn. En waarempel, ze vond aanwijzingen in de taal over het ‘vol maken’ van getallen wat waarschijnlijk verwijst naar het verdelen van de steentjes in een rij zodat er volle vakjes ontstaan als voorbereiding bij het vermenigvuldigen. En ze vond twee aanduidingen voor het getal 10: tunka en matunka. Dat laatste woord zou letterlijk vertaald “één tien” betekenen en verwijst waarschijnlijk naar het gebruik van de rechterkolom om “één te onthouden”. Deze taalkundige aanwijzingen samen met de logica van het verhaal van Leonard en Shakiban maken het wel erg waarschijnlijk dat hun beschrijving van het gebruik van de yupana overeenkomt met hoe de Inca’s dat vroeger deden. Zeker zullen we het misschien nooit weten, maar met een sterk stukje wiskunde zijn we zo dichtbij gekomen als maar mogelijk is.
Chitzen Itza / de Maya’s / de Maya-kalender
In bijna elk verhaal en elke documentaire over de Maya’s wordt wel hoog opgegeven over de wiskunde. De Maya’s worden afgeschilderd als de wiskundige genieën van de oudheid. Maar hetzelfde wordt beweerd van de oude Egyptenaren, de oude Chinezen, Babyloniërs, van vrijwel elke oude beschaving die gebouwen heeft achtergelaten waarvan de verhalenschrijvers/documentairemakers niet weten hoe ze dat hebben gedaan. Maar het bouwen van piramides en andere bouwwerken heeft helaas weinig met wiskunde te maken. Natuurlijk moeten er berekeningen gemaakt worden, en moet er logisch nagedacht worden over constructiemethoden, maar – ere wie ere toekomt – dat is architectuur of bouwkunde*. Een gebouw uitlijnen op de opkomst van de zon op een bepaalde datum of een ander astronomische gebeurtenis is ook niet echt hogere wiskunde. Het bleek nog niet zo eenvoudig om een goed wiskundig onderwerp te vinden dat gerelateerd is aan de Maya’s.
* Het gebruik van wiskunde, en dan met name meetkunde, in de bouwkunst is wel zodanig interessant dat ik daar binnenkort een verhaal over wil gaan schrijven.

Toch bleek het onderwerp achteraf voor de hand te liggen: de Maya-kalender. Onderwerp van veel misverstanden, die zelfs geleid hebben tot een film: 2012. Het idee dat de Maya’s zouden hebben voorspeld dat de wereld zou eindigen in het 2012 lijkt afkomstig van de Amerikaanse archeoloog en antropoloog Michael D. Coe, in zijn bestseller the Maya uit 1966. Misschien was het zijn achtergrond bij de CIA waardoor hij iets in de Maya-geschriften zag dat er volgens alle wetenschappers voor en na hem niet in staat. Het idee is gebaseerd op het feit dat volgens de Maya Long Count de vierde wereld is geëindigd op 21 december 2012, na 13 baktun. Hoewel dat voor de Maya’s een ontzettend belangrijke datum was, zou daarna gewoon de vijfde wereld beginnen. Maar nu wordt het tijd dat ik even wat termen uitleg.
De Maya Long Count is de jaartelling (of beter gezegd dagtelling) die de Maya’s gebruikten in hun geschiedsschrijving. Hierin werden de dagen geteld vanaf het begin van de vierde wereld. Voor dit tellen gebruikten de

Maya’s een twintigtallig stelsel met een kleine aanpassing. Eenheden werden geteld in k’in, 20 k’in zijn een winal, 18 winal zijn een tun (deze afwijking van het twintigtallig stelsel zorgt ervoor dat 18 winal = 360 dagen bijna een heel jaar vormen), 20 tun zijn een ka’tun, 20 ka’tun een bak’tun. Daarboven kan nog doorgegaan worden (zie de tabel hiernaast) maar zoals gezegd zou de vierde wereld eindigen na 13 bak’tun en daarna zou in de vijfde wereld de telling weer vanaf 1 k’in beginnen.
In het dagelijks leven telden de Maya niet met de Long Count, maar gebruikten ze andere kalenders. Opvallend is het aantal verschillende kalenders dat de Maya naast elkaar (en door elkaar) gebruikten. Zo kennen we: de Tzolk’in die met name gebruikt werd voor religieuze en ceremoniële gebeurtenissen, de Haab’ voor agrarisch gebruik, de negen Heren van de Nacht, en de Kawil: een cyclus van 819 dagen die werden aangegeven met een kleur en een windrichting. De meest gebruikte hiervan waren de Tzolk’in en de Haab’. Een dag in het leven van de Maya had zowel een Tzolk’in als een Haab’ aanduiding. De Tzolk’in bestond uit twintig perioden, aangegeven met namen, van dertien dagen, aangegeven met nummers. In totaal dus 260 dagen. De Haab bestond uit 18 ‘maanden’, aangegeven met namen, van twintig dagen, aangegeven met nummers, aangevuld met een periode van vijf dagen met een aparte naam, in totaal dus 365 dagen. Omdat elke dag zowel met een Tzolk’in-datum als met een Haab’-datum werd aangegeven, ontstond in totaal een cyclus van 18980 dagen met unieke combinaties van Tzolk’in- en Haab-data, waarna het geheel zich herhaalde (18980 is het kleinst gemene veelvoud van 260 en 365. 18980=52x365=73x260). Deze periode van 18980 dagen wordt een Calendar Round of kalenderronde genoemd en was voor de Maya’s heel belangrijk.
We hebben nu een heleboel getallen gezien, maar nog geen wiskunde. Die komt pas om de hoek kijken als we vragen gaan stellen als: waar komen die getallen vandaan? Laten we beginnen met de twee meest gebruikte: de 365 dagen van de Haab’ en de 260 dagen van de Tzolk’in. De eerste van deze twee herkennen we als bijna de lengte van ons zonnejaar of tropisch jaar[2]. Er werd lang door historici gedacht dat de Maya’s de positie van de zon niet zo precies konden meten en daarom niet wisten dat het zonnejaar eigenlijk 5 uur, 48 minuten en 45,18 seconden langer is. (Die afwijken geeft aanleiding tot onze schrikkeljaren.) Nu weten we dat de Maya’s de positie van heel veel hemellichamen heel precies konden bepalen en bijvoorbeeld de omlooptijd van de maan hadden berekend op 29.53086 dagen, met een fout van slechts 24 seconden. Alleen om één of andere reden wilden de Maya’s alleen rekenen met gehele getallen en dus schreven ze dit als 81 maancycli = 2392 dagen. Zeer waarschijnlijk gebruikten de Maya’s geen breuken omdat ze hun wiskunde al snel relateerden aan de architectuur. Zo heeft de grote tempel in Chitzen Itza – zoals ieder gids zal vertellen – aan elke zijde een trap met 91 treden, een totaal van 364. Tel daar één ‘trede’ bij op in de vorm van de tempel op de top en je krijgt de 365 dagen van het jaar, of beter gezegd van de Haab’. Er zijn niet veel geschriften van de Maya’s overgeleverd en wat er wel is is lastig te ontcijferen. Maar de laatste jaren wordt er aardig wat vooruitgang geboekt en blijkt dat de Maya’s heel goed wisten dat het zonnejaar langer was dan hun Haab’, maar ook dat het verschil een deel van een dag was. Maar blijkbaar was het gebruik van een kalander met een geheel aantal dagen belangrijker dan dat de dagen op dezelfde plek in de seizoenen vielen[3].
[2] Er wordt vaak gezegd dat dit het aantal dagen is dat de aarde erover doet om om de zon te draaien, maar dit is niet helemaal correct. Het is het aantal dagen dat de zon erover doet om op dezelfde positie ten opzichte van de sterren uit te komen, vanaf de aarde gezien. Omdat de zon ten opzichte van de sterren beweegt geeft dat een verschil met de eerste definitie – die siderisch jaar wordt genoemd – van ongeveer 20 minuten.
De 260 dagen van de Tzolk’in blijken een stuk lastiger te relateren aan omlooptijden van hemellichamen of andere astronomische zaken. Dat is door de loop der jaren door veel wetenschappers op allerlei manieren geprobeerd, maar zonder overtuigend succes. Nog niet zo lang geleden is er een nieuwe theorie bijgekomen die mij aanspreekt omdat die uitgaat van aannames die haast wel waar moeten zijn en daarop een heel mooie wiskundige redenering bouwt. De aanname waar alle min of meer mislukte pogingen op zijn gebaseerd is dat als het bij de Haab’ om een omlooptijd van de zon gaat, dan zal het bij de Tzolk’in ook wel om een omlooptijd gaan. En omdat de maan in de Maya-geschriften duidelijk op een andere manier wordt behandeld dan de zon, de planeten en de sterren, is het onwaarschijnlijk dat het iets met de maan te maken heeft. Uit de ontcijfering van een belangrijk Maya-document: de Dresden Codex, blijkt dat de Maya’s de bewegingen van Venus en Mars nauwkeurig bijhielden, dus lijkt het logisch om in eerste instantie naar deze twee planeten te kijken.
De bewegingen van Venus en Mars zijn, naast die van de zon en de maan, in veel vroege beschavingen over de hele wereld de meest belangrijke. Daar zijn twee redenen voor:
· Venus en Mars zijn vanaf de aarde het best te zien van alle planeten. Hun baan brengt ze het dichtst bij de aarde, ze staan dicht genoeg bij de zon om genoeg licht te ontvangen en terug te kaatsen, en ze staan niet te dicht bij de zon zodat ze ’s nachts goed te zien zijn.
. omdat hun baan ze het dichtst bij de aarde in de buurt brengen vertonen ze relatief vreemde banen ten opzichte van de sterren. (De naam planeten komt van het Griekse woord πλανῆται dat ‘reizigers’ betekent.) In het volgende filmpje wordt gedemonstreerd waardoor deze vreemde banen, gezien vanaf de aarde, worden veroorzaakt.

Als we de omlooptijden van de aarde, Venus en Mars bekijken is nog niet meteen een verband te zien met het getal 260. De aanname die tot een doorbraak leidt is dat als het met die periode van 260 dagen niet lukt, dat het dan misschien om de combinatie van Tzolk’in en Haab’ gaat, oftewel de Calendar Round. En nu volgt een beetje goochelen met getallen. Dat toont dat de omloopperiode van de aarde precies een geheel aantal keren in één Calendar Round past. Dat is nog niet zo verrassend, want de Calendar Round is gebaseerd op de 365 dagen van de Haab’. Maar het wordt wel verrassend als we zien de de omlooptijd van Venus precies een geheel aantal keren in twee Calendar Rounds past ( 2x18980 = 37960 = 65x584 ). En de puzzelstukjes lijken op hun plaats te vallen als we zien dat de omlooptijd van Mars precies past in drie Calendar Rounds ( 3x18980 = 56940 = 73x780 )[4]. In combinatie met de realisatie dat de omlooptijd van de aarde gelijk is, vanaf de aarde gezien, aan de omlooptijd van de zon om de aarde, betekent dit dus dat na één Calendar Round de zon op dezelfde plek staat, na twee Calendar Rounds staan de zon en Venus op dezelfde plek en na drie Calendar Rounds staan de zon en Mars op dezelfde plek. Of dit de verklaring is voor de keuze van 260 dagen voor de Tzolk’in, dat valt nog te bezien. Hopelijk komen we met het ontcijferen van de Dresden Codex en andere Maya teksten achter het antwoord. In ieder geval is zeker dat de Maya’s wel hielden van wat gegoochel met getallen en dat deze constructie hun kunsten zeker niet te boven gingen.
[4] De wat meer rekenkundig aangelegde lezers zullen al hebben gezien dat de omlooptijd van Venus dus niet een geheel aantal keren in één Calendar Round past en ook niet in drie. En de omlooptijd van Mars past niet een geheel aantal keren in één of twee Calander Rounds.
Hoe goed de Maya’s waren in rekenen en in het vaststellen van de posities blijkt wel uit het antwoord op de vraag hoe zit het nu eigenlijk met die Long Count? Of preciezer, waar hebben de Maya’s de begindatum 11 Augustus in het jaar 3114 BC op gebaseerd?

Professor Susan Milbrath van de universiteit van Florida heeft onderzoek gedaan naar de tijdrekening van de Maya’s en zij ziet een mogelijk verband tussen de Long Count en de astronomie. Uit de documenten als de Dresden Codex en de Codex Borgia – die prof Milbrath uitgebreid heeft bestudeerd – wordt duidelijk dat de Maya’s erg geïnteresseerd waren in het bijhouden van de stand van de sterren. En als je kijkt naar de sterren is er één ding dat meteen opvalt: de sterren draaien gedurende de nacht rondjes door de hemel. Natuurlijk is het eigenlijk de aarde die draait terwijl de sterren stil staan, maar vanaf de aarde gezien lijkt het of de sterren draaien. En ze draaien om een vast punt dat iedere nacht hetzelfde is.
Als we dat nu en vanuit Nederland bekijken is het vaste punt de Poolster: Polaris, waar de draaias van de aarde naar toe wijst. Maar dat punt blijkt niet altijd hetzelfde te zijn. De draaias van de aarde blijkt namelijk zelf langzaam rondjes te draaien. Dat wordt precessie genoemd en het zorgt ervoor dat het vaste punt aan de (noordelijke) sterrenhemel langzaam een rondje draait door de sterrenhemel.
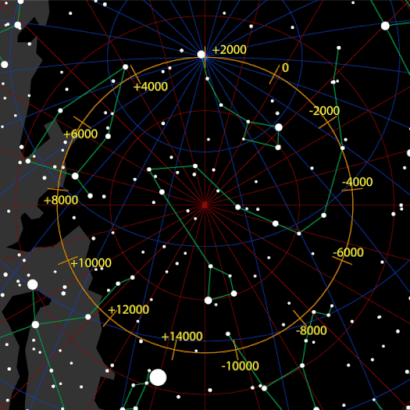
Het is eigenlijk toeval dat dat punt nu samenvalt met Polaris in het sterrenbeeld Kleine Beer. Maar als we kijken waar het vaste punt lag rond het jaar 3114 BC, dan kan het geen toeval zijn dat het toen ook samenviel met een ster, en wel Thuban in het sterrenbeeld Draco, de draak. En nu lijken de puzzelstukjes op hun plaats te vallen. Draco heeft namelijk de vorm van een slang, met een duidelijke kop en een lange staart. En wat was de belangrijkste god van de Maya’s, waaraan ze de grootste tempel in Chitzen Itza hebben gewijd? Kukulkan: de geverde slang, oftewel een slang in de lucht. Zeker zullen we het misschien nooit weten, maar als de Maya’s zo goed waren in het bepalen van de positie van de sterren, dan kunnen ze de langzame verplaatsing van het vaste punt aan de hemel, het gevolg van de precessie van de aardas, hebben opgemerkt. En als ze die hebben kunnen meten kunnen ze hebben vastgesteld dat in ongeveer 3114 BC dit punt samenviel met Thuban en rond 2012 met Polaris.
Het is moeilijk te geloven dat de Maya’s dat op het jaar precies hebben kunnen bepalen aan de hand van hun metingen. Maar als je als Maya-rekenaar tot de ontdekking komt dat tussen 31 augustus 3114 BC en 21 december 2012 precies 13 baktun, oftewel 1872000 dagen zitten… Dan kun je tot de conclusie komen dat dat geen toeval is en dat die data de begin- en einddata zijn van een tijdperk.
Waarom 31 augustus? Het kan zijn dat de Maya-sterrenrekenaars zijn uitgegaan van 21 december 2012 en van daaruit hebben teruggerekend. Tenslotte is 21 december astronomisch gezien een belangrijke dag, de kortste dag van het jaar. Dat is een mooi beginpunt voor een nieuw tijdperk. Maar daarbij moeten we er wel rekening mee houden dat de Maya’s een stuk zuidelijker leefden dan wij in Nederland, en dat vanuit hun plekje op de wereld het verschil in daglengte tussen de zomer en de winter een stuk kleiner was. Op het schiereiland Yucatan zijn er dagen die misschien astronomisch gezien interessanter zijn. Net ten zuiden van de kreeftskeerkring komt het bijvoorbeeld twee keer per jaar voor dat de zon recht boven je staat en van de zuidelijke helft van de hemel oversteekt naar de noordelijke kant. En laat één van die twee dagen nu juist 31 augustus zijn…
Ook hier zullen we misschien nooit zeker weten wat de reden was voor de keuzes van de Maya’s, maar de link met de astronomie lijkt behoorlijk zeker bij een cultuur die zoveel aandacht besteedde aan het bestuderen van de hemel. En wie weet komt er een keer een wiskundige langs die, net als bij de yupana, op basis van het beetje informatie dat we hebben tot een prachtige theorie komt die alle puntjes met elkaar verbindt.
De Chinese Muur / China / de Chinese Reststelling
China is één van de weinige landen ter wereld waar een wiskundige stelling naar genoemd is: de chinese reststelling. Op het eerste gezicht een merkwaardig wiskundig puzzeltje, dat lijkt te komen uit een puzzelboek voor jongetjes zoals ik er één was toen ik een jaar of 12 was. Maar ik zal laten zien dat vrijwel iedereen vandaag de dag regelmatig gebruik maakt van deze stelling.

De stelling is gebaseerd op een wiskundig probleem (het puzzeltje) dat is opgenomen in een boek van Sunzi (meester Sun) uit de 3e eeuw.
In die tijd kon in principe iedereen in dienst komen bij de overheid, op voorwaarde dat ze konden lezen en schrijven. Daarbij hoefden ze niet alle … karakters te kennen die de chinese taal rijk is, … was genoeg. En binnen de overheid kon je carrière maken op basis van je kennis en vaardigheden, en maakte je afkomst officieel niet uit. Natuurlijk hadden jonge mannen (tja, vrouwen telden in het oude China net zo min mee als in onze cultuur destijds) uit de beter sociale klassen betere kansen omdat ze meer tijd en geld aan studie konden besteden.
Rekenen was een belangrijke vaardigheid als je hogerop wilde komen als ambtenaar. Daarbij ging het veel meer om logisch nadenken en puzzelen (de ‘echte’ wiskunde) dan om sommetjes maken. Er bestaan dan ook nog een aantal boeken met opgaven uit vroeger eeuwen in China, waarvan het boek van meester Sun er één is.
Het probleem gaat als volgt:
Ik heb een aantal munten.
Als ik deze over drie stapels verdeel hou ik er 2 over.
Als ik deze over vijf stapels verdeel hou ik er 3 over.
Als ik deze over zeven stapels verdeel hou ik er 2 over.
Hoeveel munten heb ik?
Voor degenen die zich het rekenen van de lagere school nog herinneren is de naam van de stelling nu duidelijk. In het probleem wordt een paar keer de rest van een deling gegeven en moeten we op basis daarvan proberen te achterhalen wat het aantal munten is. Met een beetje proberen komen we op het juiste antwoord: 23 munten. Als je 23 deelt door 3 kom je op 7x3=21 en hou je 2 munten over. Als je 23 deelt door 5 kom je op 4x5=20 en hou je 3 munten over. En als je 23 deelt door 7 kom je op 3x7=21 en hou je weer 2 munten over.

Tot zover nog niet heel erg spannend en ook nog niet heel erg wiskundig. Maar dat verandert in de 13e eeuw als een groot chinees wiskundige Qin Jiushao zich afvraagt of 23 de enig mogelijke uitkomst is, en of voor alle combinaties van delers en resten het probleem een oplossing heeft. Het eerste deel van de vraag is niet zo moeilijk te beantwoorden. Je kunt namelijk bij 23 een getal optellen dat zowel deelbaar is door 3 als door 5 en door 7. Dat getal verandert de resten namelijk niet. Een dergelijk getal is altijd een veelvoud van 105=3x5x7, het kleinst gemene veelvoud van de delers. (Voor wie het leuk vindt of mij niet gelooft: reken de resten maar uit voor 128=23+105). Qin Jiushao weet te bewijzen dat er altijd een getal te vinden is, en maar één getal kleiner dan het kleinst gemene veelvoud, op voorwaarde dat de delers niet onderling deelbaar zijn.
Qin Jiushao weet dit te bewijzen door een methode te geven waarmee de oplossing gevonden kan worden, en dan aan te tonen dat deze methode altijd één enkele uitkomst geeft. Ik zal niet het hele bewijs hier geven, maar de methode uitleggen aan de hand van het probleem van meester Sun:
Zoals dat vaak gebeurt in de wiskunde beginnen we met aannemen dat we een oplossing hebben gevonden, maar dat we nog niet weten wat die oplossing is (klinkt lekker logisch toch?). We noemen de onbekende oplossing X. Deze X moet nu aan drie voorwaarden voldoen, en dat maakt het probleem lastig. Dus nu gebruiken we een techniek die ook in de politiek, in management, in het huishouden… eigenlijk overal wordt toegepast: ‘verdeel en heers’.
Divide et impera (verdeel en heers) is een Latijnse spreuk die wordt toegeschreven aan Philippus II van Macedonië (382 v.Chr.-336 v.Chr.). Philippus zou deze tactiek van verdeel en heers hebben toegepast tegen de Griekse stadstaten. De tactiek houdt in dat de ene concurrent meer rechten krijgt dan de andere concurrent. Hierdoor zal er nooit vriendschap ontstaan tussen hen beiden en hoeft de derde partij, diegene die deze tactiek gebruikt, niet te vrezen dat de eerste twee samen tegen hem zullen optreden.
De oorspronkelijke betekenis is dus heel anders – en veel minder positief – dan de betekenis die we er nu aan geven.
Deel een lastig probleem op in kleinere deelproblemen die makkelijker op te lossen zijn. We gaan X dus opdelen in drie stukken die elk maar aan één voorwaarde hoeven te voldoen.
X = A + B + C
En, omdat wiskundigen luie mensen zijn (de favoriete uitspraak van mijn wiskundeleraar in de examenklas van het VWO) gaan we ‘als je X deelt door drie hou je twee over’ een stuk korter schrijven:
X = 2 mod 3
Dit komt misschien een beetje onnatuurlijk over omdat de 3 en de 2 nu in de andere volgorde komen te staan dan in de zin ‘als je X deelt door drie hou je twee over’. (Wiskundigen zijn lui, maar niet altijd voorspelbaar.) Toch zit daar wel een logica is: je begint met het antwoord (2) en legt dan uit hoe je eraan gekomen bent (de rest bij delen door 3).
Het rijtje
X = 2 mod 3
X = 3 mod 5
X = 2 mod 7
Kunnen we nu vervangen door
X =A + B + C
A = 2 mod 3
X = 3 mod 5
X = 2 mod 7
Dit lijkt nog niet echt veel gemakkelijker. Sterker nog, het lijkt erop dat we het alleen maar ingewikkelder hebben gemaakt. In plaats van te zoeken naar één onbekend getal X moeten we nu op zoek naar drie onbekende getallen A, B en C. Maar we zijn dan ook nog maar net op weg.
De volgende stap is misschien wel de meest interessante, het is eigenlijk de ‘truc’ van het hele verhaal. Maar wiskunde is geen tovenarij, het is zelfs geen goochelarij. De ‘truc’ is gewoon een kwestie van logisch nadenken. We kunnen wel X mooi opdelen in A, B en C en zeggen dat A er nu voor moet zorgen dat er bij delen door 3 netjes de gewenste rest van 2 overblijft, maar dan moeten we er ook meteen voor zorgen dat B en C daarbij geen roet in het eten gooien. Bij het delen door 3 moeten van allebei deze getallen dus geen resten overblijven. Dat geeft
B = 0 mod 3
C = 0 mod 3
Dit kunnen we herhalen voor de andere voorwaarden, waardoor we krijgen
A = 0 mod 5
C = 0 mod 5
en
A = 0 mod 7
B = 0 mod 7
In gewone-mensen-taal staat hier dat A deelbaar moet zijn (zonder rest) door 5 en 7, B moet deelbaar zijn door 3 en 7, en C moet deelbaar zijn door 3 en 5.
Laten we nu met A beginnen. A is deelbaar door 5 en 7, wat betekent dat we A kunnen schrijven als 5x7x… We hoeven nu alleen uit te zoeken wat er op de plaats van de puntjes moet komen te staan zodat A = 2 mod 3. En nu beginnen we gewoon met zoeken bij 1. 5x7x1 = 35, als we 35 delen door 3 houden we 2 over. Bingo! Dus
A = 5x7x1 = 35.
B = 3x7x… We beginnen weer bij 1, 3x7x1 = 21, als we dat delen door 5 houden we 1 over. Dat is dus niet de juiste keuze, want we moeten 3 overhouden. 3x7x2 = 42, waarbij we 2 overhouden als we delen door 5. Ook niet goed. Maar 3x7x3 = 63 levert wel bij delen door 3 een rest 3 op, dus B = 3x7x3 = 63.
C = 3x5x… en we beginnen weer bij 1. 3x5x1 = 15 en dat levert bij delen door 7 als rest 1 op, 3x5x2 = 30 en daarmee krijgen we de gewenste rest 2, dus C = 3x5x2 = 30.

En nu zijn we klaar, want X = A+B+C = 35+63+30 = 128…. Maar dat is niet het antwoord dat we hadden verwacht. Aan het begin van dit verhaal waren we met simpel proberen uitgekomen op 23.
Voor degenen die goed hebben opgelet is het antwoord al duidelijk, en anders kun je even terug scrollen naar het plaatje van Qin Jiushao. Zijn verhaal begon met het aantonen dat je bij elk antwoord op de som van meester Sun het getal 3x5x7 = 105 mag optellen en het getal dat je dan krijgt is ook een antwoord. Maar we mogen dus van 128 ook 105 aftrekken en dan krijgen we netjes ons eerste antwoord 23.
Helemaal aan het begin van dit verhaal gaf ik aan dat vrijwel iedereen tegenwoordig de Chinese reststelling wel eens gebruikt. Nu heb ik wel lang genoeg lekker sommetjes gemaakt en wordt het tijd uit te leggen hoe dat zit. Als je wel eens gebruik maakt van een beveiligde internet-verbinding – te herkennen aan het slotje in de adresbalk en de letter https daarachter – dan is de kans groot dat de berichten die jij verstuurd of die terugkomen van de site versleuteld zijn met behulp van de Chinese reststelling. Hoe zit dat?

Stel dat ik een bericht wil sturen aan mijn bank met gegevens als mijn rekeningnummer, een bedrag dat ik over wil maken en een beveiligingscode waaraan de bank kan zien dat het bericht echt van mij komt. Als dat bericht onderschept wordt kan iemand met kwade bedoelingen – vanaf nu genaamd ‘de boef’ – een paar minuten later zelf een bericht versturen naar de bank met een opdracht om vanaf mij rekening een fors bedrag naar de rekening van de boef over te schrijven. Als mijn beveiligingscode erbij zit weet de bank niet beter dan dat dit een opdracht van mij is en ben ik een fors bedrag armer en de boef rijker. Omdat banken graag willen dat wij via internet bankieren zonder ons zorgen te hoeven maken over de boeven in de wereld, gebruiken ze allerlei methoden om te voorkomen dat wat hierboven staat kan gebeuren. Één van die methoden is het versleutelen van de berichten die via het internet heen en weer gaan tussen mij en de bank.
Één van de beste manier om een bericht te versleutelen is door gebruik te maken van een code of wachtwoord. (In principe zijn een code en een wachtwoord hetzelfde, een reeks letters, cijfers en bijzondere symbolen.) Als ik een code gebruik om mijn bericht te versleutelen kan de boef er niet achter komen wat er in staat , maar dan moet ik natuurlijk wel zorgen dat de bank mijn wachtwoord wel weet. Nu kan ik een keer bij de bank langs gaan om een wachtwoord af te spreken en dat dan blijven gebruiken. Maar, zoals iedere systeembeheerder je zal vertellen, het is verstandig om regelmatig je wachtwoord te veranderen. Hoe vaker je een wachtwoord gebruikt, hoe waarschijnlijker het wordt dat de boeven het kunnen achterhalen. Het zou het best zijn als je bij elk contact een nieuw wachtwoord zou gebruiken. Maar om nu elke keer naar de bank te gaan om een nieuw wachtwoord af te spreken… dat gaat een beetje in tegen het idee van internet-bankieren.
Het zou ideaal zijn als je iedere keer een nieuw wachtwoord zou kunnen gebruiken en de bank zou kunnen laten weten wat dat wachtwoord is, zonder naar de bank toe te hoeven. Maar ja, het wachtwoord meesturen met je opdracht is natuurlijk ook geen oplossing. Gelukkig hebben wiskundigen hier een slimme oplossing op gevonden. Een methode om elke keer een nieuw wachtwoord te kunnen genereren en de bank te laten weten wat dat wachtwoord is, maar zonder dat een boef die je bericht onderschept er achter kan komen[1]. Het klink als tovenarij, maar het is gewoon wiskunde, en wel specifiek de Chinese reststelling.
[1] Dat wiskundigen ook van essentieel belang zijn bij het kraken van een code die dagelijks veranderd, kun je goed zien in de film “The Immitation Game”.
De Chinese reststelling vertelt ons namelijk dat een combinatie van delers en resten – onder voorwaarde dat de delers niet onderling deelbaar zijn – tot een uniek getal leidt. Qin Jiushao heeft bewezen dat er altijd een unieke oplossing is die kleiner is dan het product van de delers. Dus wat doe ik nu? Ik ga bij het starten met internet-bankieren een keer naar de bank toe en spreek af welke delers we zullen gaan gebruiken. (Hierbij zorg ik ervoor dat mijn delers niet onderling deelbaar zijn. Priemgetallen zijn hiervoor heel handig.) Als ik nu een keer bij mijn rekening wil – om mijn saldo te checken, geld over te maken of wat dan ook – maak ik een wachtwoord aan dat bestaat uit een heel groot getal. (Hoe groter het getal hoe lastiger het is voor een boef om het te raden.) Maar ik moet er wel voor zorgen dat het getal kleiner is dan het product van de delers die ik met de bank heb afgesproken. Ik reken nu voor al mijn delers de rest uit voor het getal dat ik als wachtwoord heb gekozen. (Uiteraard doe ik dit niet zelf, maar mijn internet-bankieren-app doet dit voor me.) De resten stuur ik naar de bank, die daarmee – in combinatie met de delers die we hebben afgesproken – het getal kan terugrekenen dat ik als wachtwoord heb gebruikt. Volgens de Chinese reststelling – gebruik makend van de methode die ik heb laten zien – komt hier altijd één uniek antwoord uit. De bank komt dus gegarandeerd op mijn wachtwoord uit en kan mijn berichten ontsleutelen en met hetzelfde wachtwoord berichten aan mij versleutelen. Een boef die de berichten tussen mij en de bank onderschept kan hoogstens aan de resten komen, maar niet de delers en kan dus mijn wachtwoord niet uitrekenen. Zo zijn de berichten tussen mij en de bank gegarandeerd veilig, ook al worden ze door een boef onderschept.
Zo zie je maar, ook een ogenschijnlijk nutteloos wiskundig puzzeltje kan ongelofelijk nuttig blijken.
De Taj Mahal / India / Srinivasa Ramanujan
India is het land dat misschien wel het meest heeft bijgedragen aan de geschiedenis van de wiskunde van alle landen in de wereld. Helaas zijn deze bijdragen buiten de wereld van de wiskunde grotendeels onbekend gebleven. Zo zijn de getallen die wij gebruiken, en die meestal aangeduid worden als arabische getallen, oorspronkelijk afkomstig uit India. Daarom worden ze in de wiskunde tegenwoordig hindoe-arabische getallen genoemd. Één van de belangrijkste van die getallen is het getal nul. Dat lijkt een onbelangrijk getal omdat het ‘niets’ voorstelt, maar zoals prof Marcus du Sautoy in het filmpje uitlegt is wiskunde bijna niet mogelijk zonder het getal nul.
En het oudste nu bekende document waarin nul als zelfstandig getal wordt behandeld is het Bakhshali-document dat gevonden is in 1881 in Pakistan, geschreven in Sanskriet vermengd met lokale dialecten. De oudste delen van dit document dateren uit de derde eeuw en het geeft aan dat in India al in die tijd het doen van berekeningen niet voorbehouden was aan de rekenaars van de koning – zoals bijvoorbeeld bij de Inca’s – maar gebruikt kon worden door handelaren en andere ‘gewone’ mensen.

Het is lastig om aan te geven wat de belangrijkste bijdrage aan de wiskunde uit India is, maar mijn voorkeur zou niet uitgaan naar de getallen en zelfs niet naar het getal nul. Ik zou kiezen voor misschien wel het grootste wiskundige genie ooit: Srinivasa Ramanujan. Zijn leven is prachtig verfilmd in ‘The man who knew infinity’ met niemand minder dan Dev Patel en Jeremy Irons in de hoofdrollen. Net als bij films als ‘A theory of everything’ over het leven van Stephen Hawking en ‘The imitation game’ over het leven van Alan Turing, wordt in de film niet heel diep ingegaan op het werk van Ramanujan. We zien een jongeman zonder formele opleiding die een wiskundig inzicht bezit dat hij wil delen met de wereld. Vergelijkbaar met een muzikaal talent als dat van Mozart, of een schildertalent als dat van van Gogh, dat zich niet laat temperen, drijft het wiskundig talent van Ramanujan hem ertoe contact op te nemen met prof Godfrey Harold Hardy in Oxford, die zijn talent onmiddellijk herkent en hem naar Engeland haalt. De diep-religieuze Hindoe Ramanujan heeft grote moeite met de atheïstische, puur wetenschappelijke visie van Hardy.

Hardy vraagt om bewijzen, terwijl Ramanujan gelooft dat de formules hem worden ingegeven door een godin en dus niet fout kunnen zijn. Bovendien heeft Hardy als typisch wiskundige grote moeite met de menselijke kant van zijn relatie met Ramanujan. Toch zien we vanaf de eerste ontmoeting een bijzonder hechte band die vooral wordt veroorzaakt door hun gezamenlijke wiskundige blik. Hardy noemde in een interview zijn grootste bijdrage aan de wiskunde de ontdekking van Ramanujan en hun samenwerking het enige romantische incident in zijn leven.
Natuurlijk is het verhaal in de film geromantiseerd en hier en daar een beetje naast de waarheid. Zo was de vrouw van Ramanujan – Janaki – pas 10 jaar oud toen ze in 1909 trouwde met de 18-jarige Ramanujan. En toen deze zijn eerste brief aan Hardy schreef was hij al werkzaam bij de universiteit van Madras, had al meerdere artikelen gepubliceerd in de Journal of the Indian Mathematical Society, en had hij al contact gehad met andere professoren in Engeland. Hardy moet behoorlijk wat moeite doen om Ramanujan te overtuigen naar Engeland te komen, wat in 1914 uiteindelijk lukt. Al in 1916 krijgt Ramanujan zijn doctoraat en in 1918 wordt hij één van de jongste Fellows van de Royal Society ooit. Al vanaf zijn jeugd had Ramanujan gezondheidsproblemen en in de oorlogsjaren 1914-1918 lijdt hij aan vitaminetekort door zijn strikte religieuze dieet en de tekorten aan verse groenten in Engeland. In 1919 keert hij terug naar India waar hij een jaar laten overlijdt. Nu wordt gedacht dat hij misschien hepatische amoebiasis had, veroorzaakt door dysenterie in Madras. Als dit destijds was onderkend had het waarschijnlijk goed behandeld kunnen worden. Dat Ramanujan zijn formules en stellingen niet zou hebben willen bewijzen is waarschijnlijk een mythe die gebaseerd is op het feit dat hij in zijn notitieboeken geen bewijzen geeft. Maar dat kan verklaard worden uit het feit dat het in India normaal was om, vanwege de kosten van papier, stellingen uit te werken op een lei en alleen het resultaat op papier te zetten. Een andere onderbouwing voor deze mythe is de nadruk die Hardy legt op bewijsvoering. Maar die kan weer verklaard worden door een campagne die Hardy in Engeland voerde voor een striktere bewijsvoering, gebaseerd op het werk van de Franse, Zwitserse en Duitse wiskundigen uit die tijd.

Het is ook voor mij lastig om aan te geven waar het werk van Ramanujan uit bestaat. Een veel aangehaald voorbeeld is zijn formule:
Misschien is het niet meteen zichtbaar, maar dit is een ‘recept’ waarmee het getal π kan worden berekend, een heel belangrijk getal in heel veel takken van de wiskunde[1]. De eerste benaderingen van dit getal komen – voor zover bekend – van Archimedes, die kwam met 223/71 < π < 22/7. Archimedes gebruikte hiervoor figuren met 96 zijden die precies in en precies om een cirkel pasten. De schatting van Archimedes komt neer op 3.1408450… < π < 3.142857. Zoals te zien zijn de eerste twee cijfers achter de komma van de gegeven getallen gelijk en daarna gaan ze verschillen. De schatting van Archimedes is dus nauwkeurig tot twee getallen achter de komma. In de derde eeuw was het een Chinese wiskundige – Liu Hui – die met een methode kwam waarmee π in principe tot elke gewenst aantal cijfers achter de komma kon worden berekend. In de vierde eeuw gebruikte Zu Chongzhi deze methode om π tot 6 cijfers achter de komma uit te rekenen. De berekening was echter enorm ingewikkeld en gebaseerd op figuren met 12288 zijden.
[1] vreemd genoeg speelt het getal π een ontzettend belangrijke rol in de kansrekening.

Pas in de 14e eeuw was het een Indiaas wiskundige Madhava van Sangamagrama die met een formule kwam in de vorm van een oneindige reeks.
Het grote voordeel hiervan is dat elk van de termen relatief eenvoudig te berekenen is en dat als je meer cijfers achter de komma wilt, je niet helemaal overnieuw hoeft te beginnen. Er zijn meer van dit soort reeksen waarin π kan worden uitgedrukt en de formule van Ramanujan is er ook één. (Het symbool ∑ staat voor een oneindige som.)
De formule van Madhava van Sangamagrama heeft het voordeel dat de termen veel simpeler zijn dan in die van Ramanujan, maar ze heeft ook een nadeel. Er zijn veel meer termen nodig om hetzelfde aantal cijfers achter de komma goed te krijgen. De formule van Ramanujan blijkt één van de snelste en levert per extra term maar liefst 8 extra correcte cijfers achter de komma op! In de meeste computers wordt de formule van Ramanujan dan ook gebruikt om π uit te rekenen.
Tijdens zijn leven produceerde Ramanujan een ongelofelijk aantal van wel 3900 nieuwe stellingen en formules. Sommige daarvan zijn zo uniek en ongekend dat ze tot nieuwe onderzoeksgebieden in de wiskunde hebben geleid. Één van de grootste doorbraken in de wiskunde van de afgelopen jaren is het bewijs dat Andrew Wiles in 1994 leverde van de laatste stelling van Fermat. In het onderstaande fragment (uit de BBC-documentaire-serie Horizon) is goed te zien hoe belangrijk wiskunde voor een wiskundige kan zijn.
Dit werk zou niet mogelijk zijn geweest zonder het Ramanujan-vermoeden en het daarop gebaseerde werk aan elliptische vormen.
In de film wordt een aardige anekdote gegeven over zogenaamde ‘cab-numbers’ (taxi-getallen). Hardy maakt een opmerking over het nummer van een taxi die hij heeft genomen en noemt het getal erg saai.

Daarop zegt Ramanujan dat het juist een heel interessant getal is: 1729, omdat het het kleinste getal is dat op twee verschillende manieren geschreven kan worden als de som van twee derde machten:
Deze anekdote wordt door Hardy zelf beschreven als een voorbeeld van de relatie die Ramanujan had met getallen. Volgens Hardy had zijn collega John Edensor Littlewood gezegd dat het wel leek alsof ieder getal een persoonlijke vriend van Ramanujan was.
In 1976 werd een nog onbekend notitieboek van Ramanujan gevonden waar tot vandaag de dag door wiskundigen over de hele wereld aan wordt gewerkt. Waar het werk van Ramanujan allemaal nog meer toe gaat leiden is niet te voorspellen, maar duidelijk is wel dat Ramanujan een bijzonder persoon was met een bijzonder talent voor wiskunde. En ‘The man who knew infinity’ is een prachtige film die een mooi beeld geeft van een bijzonder relatie tussen Ramanujan en zijn mentor en grootste bewonderaar Hardy…
(En ja, natuurlijk, ik heb de film inmiddels in de kast staan en bijna ademloos bekeken ;-))
Petra / Jordanië / Arabische wiskunde
Zoals ik in het verhaal over India al aangaf hebben we in het westen veel van onze kennis over de wiskunde uit India te danken aan de Arabieren. Maar ook de werken van onze ‘eigen’ grote Griekse wiskundigen als Pythagoras, Euclides en alle anderen hadden we waarschijnlijk niet gekend zonder de Arabische gouden eeuw, de bloeitijd van de Arabische wetenschap en met name de wiskunde.

Helaas is veel van de geschiedsschrijving over de Arabische gouden eeuw sterk religieus beïnvloed, waardoor moeilijk vast te stellen is wat de waarheid is. Maar voor zover ik kan achterhalen legt kalief Harun al-Rashid (‘Aäron de Rechtvaardige’) aan het eind van de 8e eeuw de basis voor het ‘Huis van de Wijsheid’ met het aanleggen van een privé-bibliotheek in Bagdad. Op zijn leven zijn veel van de verhalen van duizend en één nacht gebaseerd. Al vrij snel ziet Harun zich genoodzaakt van Raqqa in Syrië zijn hoofdstad te maken om opstanden in zijn rijk het hoofd te kunnen bieden. Zijn zoon Abu al-Abbas al-Maʾmūn ibn Hārūn al-Rashīd maakte van de bibliotheek een soort universiteit, en bracht wetenschappers vanuit zijn hele rijk daar samen.

Zelf was al-Mamun onder andere geïnteresseerd in cartografie. Hij liet metingen uitvoeren om de omtrek van de aarde vast te stellen. (Eigenlijk waren de metingen bedoeld om de lengte van een aardse graad vast te stellen. Met behulp daarvan kwamen de Arabieren uit op een omtrek van de aarde van 40.253,4 km. De echte waarde is 40.075,8 km. Interessant is dat in India de wiskundige Aryabhata in het begin van de 6e eeuw al uitgekomen was op 39968 km, wat dichterbij de werkelijke waarde komt.) Ook liet hij een kaart maken van de Arabische wereld die o.a. aantoont dat de Arabische zeelieden veel verder de open zee op konden varen dan hun Europese collega’s. Dat kan alleen verklaard worden als ze beter konden navigeren. Verder ontwikkelde de alchemie zich sterk onder de hoede van al-Mamun, wat leidde tot nieuwe geneesmiddelen door Jabir Ibn Hayyan. En tenslotte leidde al-Mamun nog vlak voor zijn dood een expeditie naar Egypte waar hij probeerde in de schatkamers van de Grote Pyramide van Gizeh te komen. (De huidige toeristeningang is oorspronkelijk de tunnel die de kalief in 832 liet graven.)
In het Huis der Wijsheid werden werken van Griekse wetenschappers, de Egyptenaren, Chinezen en Indiërs samengebracht en vertaald. We hebben het aan de Arabieren te danken dat veel van de werken van de Griekse wetenschappers bewaard zijn gebleven, want tijdens de Arabische gouden eeuw werden overal in Europa boeken van Plato, Aristoteles, Euclides enzovoorts verbrand omdat ze geschreven waren door heidenen. De Arabieren voegden zelf ook heel veel toe aan de kennis die ze ‘erfden’ van andere beschavingen. Helaas kennen we veel meer namen van Griekse dan van Arabische (of Indiase of Chinese) wetenschappers, maar in heel veel wetenschappelijke termen is de Arabische oorsprong gelukkig nog te herkennen. Simpel gesteld zijn (vrijwel) alle termen die met ‘al’ beginnen afkomstig van een Arabische wetenschapper of Arabisch woorden. Het eerder genoemde woord alchemie komt uit het Arabisch, maar ook alcohol, almanak, elixer, en natuurlijk algoritme en algebra. En verder hebben heel veel namen van sterren een Arabische oorsprong.

Een voorbeeld van een belangrijke bijdrage van de Arabische wereld aan de wiskunde is de door Muhammad al-Karaji bedachte methode van bewijzen met inductie. Vaak worden in de wiskunde stellingen bedacht waarvan we denken dat ze altijd kloppen. Voor kleine getallen kunnen we dat vaak makkelijk zien of controleren. Maar hoe tonen we nu aan dat de stelling altijd klopt, voor alle getallen? Een voorbeeld: als we opeenvolgende oneven getallen bij elkaar optellen komt er kwadraat uit. 1 is een kwadraat (van 1), 1+3=4 is een kwadraat (van 2), 1+3+5=9 is een kwadraat (van 3). We vermoeden nu dat 1+3+5+…+(2n-1)=n2. (Als ik bijvoorbeeld de eerste 4 oneven getallen neem is het hoogste 7=2x4-1. In het algemeen geldt dat bij n oneven getallen het hoogste altijd de waarde 2n-1 heeft. En de som is niet alleen een kwadraat, maar het kwadraat van n, het aantal termen dat ik optel.) Maar hoe bewijzen we nu dat de formule altijd klopt, voor alle aantallen n? Er zijn oneindig veel getallen n, dus allemaal proberen heeft geen zin. De methode van al-Karaji biedt de oplossing. We beginnen bij n=1, waarbij we heel simpel zien dat we maar één term hebben, namelijk 1, en die is gelijk aan het kwadraat van 1. Dus voor het kleinste getal dat we kunnen kiezen (1) klopt de formule. De volgende stap is laten zien dat als de formule voor een willekeurig getal k klopt, hij dan automatisch ook voor het getal k+1 (dus één groter dan k) geldt. Dat doen we door de formule voor k+1 op te schrijven:

Dit gaan we uitschrijven en omschrijven, waarbij we als eerste gebruiken dat we mogen aannemen dat de formule klopt voor het getal k, dus:

Dat betekent dat we de som aan de linkerkant kunnen vervangen door k2, op de laatste term na:

Aan beide kanten de haakjes wegwerken levert

Nu is het laatste stapje makkelijk, nog even de 2 en de -1 links samen nemen

We komen uit op een waarheid als een koe en dus hebben we nu bewezen dat als de formule klopt voor het getal k, dan klopt die ook voor k+1. Omdat we ook een beginpunt hebben waarvoor de formule klopt (n=1) kunnen we met deze stap alle getallen doorlopen tot in het oneindige en hebben we dus bewezen dat de formule voor alle getallen klopt. Deze bewijsmethode is ongelofelijk krachtig en belangrijk in de wiskunde.

Het Huis der Wijsheid kende een grote bloei onder al-Mamun en zijn opvolgers, en in het midden van de 9e eeuw had het de grootste verzameling boeken ter wereld, waaronder de beste vertalingen van werken van o.a. Archimedes en Euclides. De kaliefen zorgden ervoor dat de wetenschappers vrijwel altijd een dubbelfunctie hadden. Naast hun wetenschappelijke werk werden ze ingezet als architecten en opzichters bij grote bouwprojecten, werden ze adviseurs ingezet om ingewikkeld technische, militaire en bestuurlijke problemen op te lossen, waren ze verantwoordelijk voor het opstellen en bijhouden van kalenders en werkten ze in het ziekenhuis van Bagdad. Om te zorgen voor een open en wetenschappelijke houding en om religieuze conflicten buiten de deur te houden introduceerde al-Mamun het Mutazilisme als de officiële theologie en dwong alle wetenschappers een eed af te leggen waarin ze zwoeren de principes van het Mutazilisme hoog te houden. Al-Mumun richtte zelfs een soort inquisitie op die tegenstanders vervolgde. De uitgangspunten van deze inquisitie waren nogal wat ander dan die van de inquisitie die de katholieke kerk in Europa in de 12e eeuw oprichtte. Één van de belangrijkste principes van het Mutazilisme was namelijk dat als religieuze teksten en doctrines in strijd waren met de logica, dan waren de teksten en doctrines fout. De logica was altijd leidinggevend, wat een enorme vrijheid bood aan wetenschappers en toestond dat mensen met verschillende religieuze achtergronden samen konden werken aan het oplossen van problemen en het doen van nieuwe ontdekkingen. Het is duidelijk dat al-Mamun een aanhanger was van de Griekse filosofen en met name Aristoteles.
Hoewel de houding van al-Mamun dus erg open was en het Huis der Wijsheid geleerden met verschillende achtergronden toeliet, was er wel één duidelijke restrictie: vrouwen waren niet welkom. In mijn verhalen over de oorsprong van de TaNaKh, de bijbel en de Qu’ran beschrijf ik de nauwe samenhang tussen het Joodse en Christelijke geloof en de Islam, die vanwege hun gedeelde geschiedenis ook veel ideologie delen. We weten dat in de Griekse en Egyptische samenlevingen vrouwen belangrijke bijdragen leverden aan de wetenschap. Dat de drie monotheïstische godsdiensten allemaal vijandig staan tegenover wetenschap en vrouwen – en dus helemaal op de combinatie van beide – is waarschijnlijk te verklaren door het feit dat ze alledrie hun geschiedenis terugvoeren op het verhaal van Abraham. Diens vrouw Sara is degene die uitspraken van Jahweh/God/Allah in twijfel trekt omdat ze niet logisch zijn. (De afstammelingen van Abraham zullen het uitverkoren volk vormen, maar Sarah is te oud om kinderen te krijgen. Sarah legt uit dat dat niet

logisch is en stelt voor dat Abraham een kind moet krijgen met haar bediende Hagar. Als Jahweh/God/Allah zijn belofte aan Abraham dat hij met Sarah een kind zal krijgen herhaalt moet zij daar in zichzelf om lachen en daar is Jahweh/God/Allah niet blij mee.)
Pas als Abraham zijn ware geloof toont door tegen alle logica in te gaan (Jahweh/God/Allah vraagt hem zijn zoon te offeren, waardoor er geen afstammelingen zullen zijn en dus geen uitverkoren volk) sluit Jahweh/God/Allah opnieuw zijn verbond met Abraham (en spaart natuurlijk diens zoon Isaac). Ook in het scheppingsverhaal is het Eva die – opgehitst door de slang – de logica betwijfelt van het verbod van Jahweh/God/Allah om te eten van de vruchten van de boom van de kennis van goed en kwaad. (Overigens wordt de vijandige houding tegenover wetenschap, het vergaren van kennis, nog verder aangejaagd door de naam van de boom af te korten naar ‘boom der kennis’).

Een gruwelijk voorbeeld van de vijandige houding van – in geval de christelijke – fanatieke gelovigen tegenover vrouwen in de wetenschap is wel de moord op Hypatia, een 4e eeuws filosofe, astronome en wiskundige in Alexandrië. Ze had de pech betrokken te raken bij een conflict tussen de Romeinse prefect Orestes en bisschop Cyrillus van Alexandrië. Deze laatste had in 414 alle Joden uit de stad verbannen en hun bezittingen geconfisqueerd. Orestes had daartegen geprotesteerd en vroeg Hypatia om te bemiddelen in het conflict omdat ze in de stad een enorme reputatie had vanwege haar onfeilbare logica. Cyrillus gebruikte de hiervoor genoemde vijandige houding van het geloof tegenover vrouwen en logica – en zeker vrouwen die logica gebruikten – om aan de fanatiek Christelijke groepering van de parabalani uit te leggen dat Hypatia dus wel contact moest hebben met de duivel. Opgehitst door de verhalen van Cyrillis en hun fanatisme overvielen de parabalani de koets van Hypatia, sleepten haar een kerk binnen, trokken de kleren van haar lijf en vermoordden haar. Ze scheurden haar lichaam in stukken, sleepten deze door de stad en verbrandden ze. De vijandige houding van de abrahamistische religies tegenover vrouwen in de wetenschap zien we helaas tot op de dag van vandaag terug, hoewel gelukkig de verhouding tussen vrouwen en mannen in de wetenschap in snel tempo gelijk aan het trekken is.

(In Amerika kon je het in de 20e eeuw nog net een stapje ongelukkiger treffen dan een vrouw te zijn in de wetenschap: een zwarte vrouw zijn in de wetenschap. Toch hebben zwarte vrouwen onder andere een belangrijke bijdrage geleverd aan het Amerikaanse ruimtevaart-programma. Een mooie film hierover is “Hidden figures”.)
Ook in de Arabische wereld won uiteindelijk het (islamitisch) fanatisme het van de wetenschap. Toen de Mongolen in 1258 de boeken uit de beroemde bibliotheek in de rivier de Tigris gooiden was de Arabische gouden eeuw al lang voorbij en regeerde het fundamentalisme. Gelukkig had de kennis die behouden en uitgebouwd was in het Huis der Wijsheid inmiddels een ander onderdak gevonden door de opkomst van de Renaissance in Italië, het volgende land van onze wereldreis.
Rome / Italië / Leonardo van Pisa
We zijn aangekomen bij de laatste stop van onze wereldreis en dus het laatste verhaal. En dat verhaal gaat over de – na Galileo Galilei – bekendste Italiaanse wiskundige. Maar zelfs de meeste wiskundigen zullen hun wenkbrauwen optrekken bij de naam Leonardo van Pisa. We kennen hem namelijk onder de naam die hem pas in 1838 door een Frans historicus is gegeven: ‘zoon van Bonacci’, ofwel ‘filius Bonaccis’ afgekort tot Fibonacci. Helaas kennen de meeste mensen zijn naam – die dus niet eens zijn echte naam is – alleen omdat de reeks getallen die zijn naam draagt wel eens in een film gebruikt wordt.
Wie de man was, wat hij voor de wiskunde heeft betekend en hoe hij aan die beroemde reeks getallen is gekomen, daar gaat dit verhaal over.

Leonardo van Pisa werd in 1175 geboren, maar waarschijnlijk niet in Pisa en zijn vader heette geen Bonacci maar Guglielmo. Hij was wel van de Bonacci familie, die zeer invloedrijk was in Pisa. Welke positie Guglielmo precies had in de politiek van Pisa is niet helemaal duidelijk, maar hij vertegenwoordigde in ieder geval de handelsbelangen van de familie in Noord Afrika in de stad Bugia (nu Béjaïa in Algerije). De stad was onderdeel van het kalifaat van de Almohaden, een Berberse moslimstroming*. Daar ging de jonge Leonardo naar school en leerde het cijfersysteem dat we nu kennen als de Hindu-Arabische getallen. Hij had een aanleg voor en interesse in wiskunde en kwam er al snel achter dat in de Arabische wereld een schat aan wiskundige kennis aanwezig was, zoals ik in het verhaal over de Arabische wiskunde heb uitgelegd. Misschien realiseerde de jonge Leonardo zich dat het opkomend fundamentalisme in de Arabische wereld een bedreiging vormde voor deze kennis, of misschien zag hij alleen maar in dat deze kennis in een handelsfamilie heel goed van pas kan komen.
* Interessant is dat de naam Almohaden is afgeleid van het Arabische al-Moahhidoen, wat “de monotheïsten” betekent, wat doet vermoeden dat er ook polytheïsten onder de moslims waren in die tijd. Voor meer informatie over de geschiedenis van de islam zie mijn verhaal over wie de qu'ran schreef.

Hoe het ook zij, Leonardo was rond 1200 terug in Pisa en bracht in 1202 een boek uit dat hem beroemd zou maken: het Liber Abaci (Boek van de abacus, of het boek van de berekeningen). In dit boek legt hij uit hoe met de Hindu-Arabische getallen veel makkelijker gerekend kan worden dan met de Romeinse getallen die op dat moment in Europa werden gebruikt. Daarna legt hij uit hoe dat gebruikt kan worden om gewichten en maten om te rekenen (in Europa werden nogal wat verschillende meetsystemen gebruikt in die tijd), hoe je rente kon berekenen en doorrekenen, en een aantal andere toepassingen. Uit de toepassingen en voorbeelden die Leonardo geeft wordt duidelijk dat hij vanuit een handelsgeest schreef en zijn werk werd de basis voor de snelle groei van het bankensysteem in Europa, dat weer de Renaissance aanwakkerde (en voor een deel zelfs mogelijk maakte). Maar hij geeft aan het eind van zijn boek ook een uitleg over irrationele getallen (getallen die niet als breuk geschreven kunnen worden, zoals π waar ik het in het verhaal over India over heb gehad) en priemgetallen (getallen die alleen deelbaar zijn door zichzelf en door 1 en die heel belangrijk zijn bij codering met bijvoorbeeld de Chinese reststelling). Dat waren op dat moment zuiver wiskundige begrippen zonder enige toepassing. Ook uit de latere levensloop van Fibonacci wordt duidelijk dat hij een echte wiskundige was en niet alleen een slimme handelaar die in wiskunde alleen een middel zag om nog slimmer te handelen.
Het Liber Abaci werd al snel een bestseller in Europa, vooral vanwege de praktische toepassingen. Het rekenen met Hindu-Arabische getallen was zoveel makkelijker dan met Romeinse cijfers dat – zoals gezegd – de internationale handel en de banken een enorme groei doormaakten. In 1220 brengt Leonardo zijn tweede boek uit: Practica Geometriae, met technieken voor landmeting, positiebepaling en het berekenen van oppervlakten en volumes. We weten weinig over de tussenliggende periode in zijn leven, maar het onderwerp van twee van zijn werken die verloren zijn gegaan – di minor guisa, over handelsrekenen, en een commentaar op het werk van Euclides – doet vermoeden dat hij geïnteresseerd bleef in zowel de praktische als de theoretische kant van de wiskunde. Het onderwerp van Practica Geometriae wijst erop dat hij inmiddels bekend was geworden en zich in hogere politieke krijgen ophield. In 1225 dringen de wetenschappelijke adviseurs van keizer Frederik II er bij de keizer op aan dat hij Leonardo moet ontmoeten tijdens een bezoek aan Pisa. De legende gaat dat de keizer eerst wel eens wilde weten of Leonardo echt zo slim was of dat hij alleen maar goed was in het vertalen van de werken van de Arabieren. Daarom gaf hij zijn ‘hofwiskundige’ Johannes van Pisa de opdracht om een aantal wiskundige opgaven te bedenken die hij Leonardo kon voorleggen. Één van die opgaven was het konijnenprobleem waarvan de oplossing tot de beroemde Fibonacci-reeks leidde.
Wiskundigen die de geschiedenis van Fibonacci hebben bestudeerd weten dat dit verhaal niet klopt. Keizer Frederik II was erg geïnteresseerd in wetenschap en liet werken van Griekse en Arabische geleerden vertalen aan zijn hof. Hij heeft zelf een boek geschreven over valkenierschap in een wetenschappelijke stijl. En er wordt beweerd dat hij experimenten liet uitvoeren die tegenwoordig niet door een ethische commissie zouden komen. Zo wilde hij testen of het Hebreeuws, het Grieks, Latijn of Arabisch de oudste taal was, door kinderen te laten opgroeien zonder ze bloot te stellen aan taal. De kinderen werden afgesloten van de buitenwereld opgevoed door pleegouders die instructie kregen nooit te praten als de kinderen hen zouden kunnen horen. Volgens de monnik die de experimenten heeft beschreven mislukten deze omdat de kinderen begonnen te klappen, gebaren en communiceren met gezichtsuitdrukkingen. Nu zouden we dat misschien een elementaire vorm van gebarentaal noemen.
Hoe dan ook, het is onwaarschijnlijk dat Frederik II moest worden overgehaald om Leonardo te ontmoeten. Maar dat Johannes van Palermo hem problemen heeft voorgelegd om te testen of hij alleen maar het werk van de Arabieren vertaalde klopt wel. Leonardo heeft in 1225 het boek Flos uitgebracht, waarin hij aangeeft dat dit boek de antwoorden bevat op drie van die opgaven. Interessant is dat één van die opgaven is het vinden van een oplossing voor de vergelijking 10x + 2x2 + x3 = 20. Het is interessant omdat deze opgave rechtstreeks uit een boek van de Arabische wiskundige Omar Kayyam komt, die ook de oplossing geeft. Leonardo beschrijft echter in zijn boek dat hij de vergelijking niet kan oplossen met de hem bekende methodes, bewijst dat ook en geeft vervolgens een benadering van de oplossing die tot 9 cijfers nauwkeurig is. Voldoende bewijs dat hij niet kopieerde wat de Arabieren hadden bedacht, maar dat hij zelf een groot wiskundige was.
We weten helaas ook dat het konijnenprobleem niet één van de opgaven was. Leonardo noemt dit probleem en de oplossing namelijk al in zijn Liber Abaci. Maar het probleem en de oplossing komen waarschijnlijk niet eens van Leonardo. In ieder geval was de reeks die nu bekend staat als de Fibonacci-reeks al bekend in India in de 6e eeuw. Maar het blijft wel een mooi verhaal.

Fibonacci omschrijft het probleem zelf als volgt:
Een zeker man stopt een paartje konijnen in een ruimte die aan alle kanten is afgesloten. Hoeveel paar konijnen zijn er na een jaar als we aannemen dat elk paar iedere maand een nieuw paar baart dat vanaf de tweede maand zelf vruchtbaar wordt?
Ik kan me voorstellen dat dit – zeker voor niet-wiskundig-getrainden – niet onmiddellijk duidelijk is. Dus zal ik het probleem (hopelijk) wat duidelijker uitleggen.
Stel we beginnen met een paartje konijnen dat pas is geboren. Natuurlijk voeren we die lieve beestjes goed en we zorgen ervoor dat ze een fijn leventje hebben in een mooi hokje. Na een maand zijn deze konijntjes vruchtbaar. (Daarmee is het wel een heel bijzonder soort konijnen, want normaal duurt dat 3 tot 5 maanden. Maar ja, in de wiskunde is het soms net als in sprookjes, alles is mogelijk.) En omdat het konijnen zijn maakt het mannetje meteen van de gelegenheid gebruik en raakt het vrouwtje meteen in verwachting (bij dieren noemen we dat natuurlijk ‘drachtig’). Een maand later worden er twee jonge konijntjes geboren, en heel toevallig weer een mannetje en een vrouwtje. (Ook dat is wat vreemd, want normaal gesproken bestaat een ‘worp’ uit 8 tot 12 jongen.) Het nieuwe paartje zetten we apart in een hokje en het ouder-paartje gaat meteen verder met de voortplanting. De volgende maand worden opnieuw twee konijntjes geboren, en – je verwachte het misschien niet – weer een mannetje en een vrouwtje die weer hun eigen hokje krijgen. Een maand later krijgt het ouder-paartje weer jongen, maar nu komt er ook een paartje jongen bij hun eerste worp die de maand daarvoor (op een leeftijd van 1 maand) vruchtbaar zijn geworden.
Het vruchtbaar worden na een maand, jongen krijgen na een maand, apart zetten en weer opnieuw jongen krijgen na een maand verloopt elke keer bij elk paartje precies hetzelfde. Er gaan geen konijnen dood en er komen geen konijnen van buitenaf bij. Het is allemaal een beetje gekunsteld, maar dat vinden wiskundigen vaak niet erg. Ze vinden de vraag en het benodigde denkwerk veel te leuk. De vraag in dit geval is hoeveel paartjes konijnen er na een jaar zijn. (Of anders gezegd, hoeveel aparte hokken zijn er nodig?)

Een veel gebruikte methode in de wiskunde is om eerst maar eens te beginnen met de boel uit te tekenen. In het plaatje hiernaast zie je bij elke maand hoeveel konijntjes er zijn aan het eind van die maand. Natuurlijk beginnen we bij maand 0. Om te beginnen hebben we één paartje, na een maand nog steeds, bij maand 2 is er één paartje bij gekomen dus zijn er twee paartjes in totaal, bij maand 3 zitten we op 3 paartjes, bij maand 4 op 5 en bij maand 5 op 8. Maar zo langzamerhand wordt het uittekenen wel erg veel werk, en wiskundigen houden niet van veel werk. Dus wordt het tijd om te gaan kijken of we een systeem kunnen ontdekken. En natuurlijk kan dat.

Iedere maand bestaat het aantal konijnen uit twee delen: de konijnen die er de vorige maand waren en de konijnen die er nieuw zijn bijgekomen. Het aantal paartjes is dus het aantal paartjes van vorige maand plus het aantal paartjes dat deze maand is geboren. Dat laatste aantal is gelijk aan het aantal vruchtbare paartjes in de vorige maand. En dat is weer gelijk aan het aantal paartjes dat toen minimaal een maand oud was. En dat is weer gelijk aan het aantal paartjes dat er de maand daarvoor was.In het plaatje hiernaast heb ik geprobeerd dat met kleuren aan te geven. De konijnen bij maand 5 hebben twee kleuren: blauw en geel. De blauwe konijnen zijn dezelfde als in maand 4. De gele konijnen zijn de jongen van de groene konijnen in maand 4 (de groene konijnen in maand 4 zijn zowel blauw als geel, groen dus). En de groene konijnen in maand 4 zijn weer dezelfde als de gele konijnen in maand 3.
Dus het aantal paartjes in maand 5 kunnen we uitrekenen door het aantal paartjes van maand 4 en het aantal paartjes in maand 3 bij elkaar op te tellen. En dat geldt voor elke volgende maand ook, we krijgen het aantal in een maand door de aantallen in de twee voorafgaande maanden bij elkaar op te tellen. Als we weten met hoeveel paartjes we beginnen kunnen we dus met dit ‘recept’ (algoritme) doorrekenen naar elke willekeurige maand.
We kunnen het recept ook in een formule vangen:
kn = kn-1 + kn-2
waarbij de letter k staat voor het aantal konijnen, en het subscript (het kleine lettertje dat er onderaan bungelt) n staat voor het nummer van de maand. Nu kunnen we uitrekenen op hoeveel paartjes we zitten na een jaar, dus op maand twaalf*. De Fibonacci-reeks ziet er namelijk zo uit:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, …
en daarvan moeten we de 13e term hebben (de eerste term is maand 0, de tweede maand 1 enzovoorts), oftewel 233.

Zoals ik aan het begin van dit verhaal aangaf is Fibonacci vooral bekend geworden door deze reeks getallen. Die bekendheid heeft waarschijnlijk te maken met het eenvoudige recept en de lekker klinkende naam. Binnen de wetenschap heeft de interesse die de reeks van Fibonacci de laatste jaren krijgt een hele andere oorzaak. (Waarmee ik niet wil beweren dat wetenschappers niet gevoelig zijn voor eenvoud en lekker bekkende namen.) De reeks blijkt in de biologie op te duiken op allerlei plekken waar we die niet meteen zouden verwachten. Als we bijvoorbeeld tellen hoeveel blaadjes een bloem heeft dan komen we in heel veel gevallen op een getal uit de Fibonacci-reeks. Ook het aantal spiralen in zaadjes in het hart van een zonnebloem, in de schubben van een dennenappel of in de roosjes van een bloemkool, overal blijken we op getallen uit te komen die voorkomen in de Fibonacci-reeks. Dit is geen teken van ‘intelligent design’ of een mystieke boodschap die verstopt is in bloemkolen, het is simpel logica. Het heeft ermee te maken dat een plant ‘zoekt’ naar een verdeling van bloemblaadjes, zaden, schubben, roosjes of andere zaken volgens een simpele regel. Bijvoorbeeld: zo min mogelijk overlap, zo veel mogelijk in zo min mogelijk ruimte, simpele concepten of regels die de groeikernen in een plant volgen (en die weer simpel gebaseerd blijken te zijn op bijvoorbeeld de concentratie groeihormonen). Het is wat lastig precies uit te leggen, maar als je het echt wilt weten geven deze filmpjes misschien een goed startpunt.
In ieder geval brengt het onderzoek naar Fibonacci-getallen in de natuur naar voren dat wiskunde overal in de natuur opduikt. In de natuurkunde was al heel lang duidelijk hoe belangrijk de wiskunde met haar formules en methodes is voor het beschrijven van allerlei verschijnselen van de beweging van planeten tot de kleinste deeltjes, van oceaanstromingen, het weer, de sterkte van gebouwen en bruggen… Overal gebruiken we formules en dus wiskunde, en wiskundige methodes om die vergelijkingen op te lossen. Natuurlijk zijn computers en informatica gebaseerd op wiskunde, maar ook in de biologie, de psychologie en eigenlijk in alle wetenschappen wordt steeds meer wiskunde gebruikt. (In mijn verhaal over de verkeerde wiskunde leg ik uit dat de logica, één van de belangrijkste onderdelen van de wiskunde, de basis vormt voor alle wetenschap.) Nu gaan er stemmen op – vooral onder fundamenteel natuurkundigen – dat wiskunde wel eens meer zou kunnen zijn dan alleen een heel krachtig en nuttig instrument om alles om ons heen te beschrijven. Het zou wel eens zo nuttig en krachtig kunnen zijn omdat alles om ons heen ‘gemaakt’ is van wiskunde. Dat klinkt heel gek, maar als je je verdiept in de fundamentele natuurkunde, en dan met name de kwantummechanica, dan lijkt het erop dat als je maar ‘diep’ genoeg in de hele hele hele kleine deeltjes ‘kijkt’ er eigenlijk geen deeltjes meer zijn maar alleen nog maar formules, waarschijnlijkheden en logica. Zo zou wiskunde wel eens ‘the fabric of our universe’ kunnen zijn….
Dit verhaal eindigt hier, de reis is compleet, we zijn de wereld rond. Maar natuurlijk houdt de wiskunde niet op en dus de verhalen ook niet. Dus als je het interessant vond, er volgt vast nog een keer meer 😉.
